Bayesian updates from negative genetic results
I recently had a genetic panel done. Hundreds of genes were tested and I came back as a carrier for a couple of things. This isn't surprising:
- Lazarin et al (2012) find that "24% of individuals were identified as carriers for at least one of 108 disorders, and 5.2% were carriers for multiple disorders".
- Fridman et al (2021) find that "based on 6,447 exome sequences of healthy, genetically unrelated Europeans of two distinct ancestries, we estimate that every individual is a carrier of at least 2 pathogenic variants in currently known autosomal-recessive (AR) genes and that 0.8%–1% of European couples are at risk of having a child affected with a severe AR genetic disorder.
Updates from positive tests
One of the genes I'm a carrier for is associated with Glycogen storage disease type II.
Knowing I'm a carrier means it's straight-forward to use Mendelian genetics to determine that my siblings have a 50% chance of being carriers and my niblings have a 25% chance of being carriers.
The background incidence of this mutation is ~1 in 530, which are also the odds a partner would be a carrier. If we had a child, there'd be a 25% chance said child would inherit the mutation from both of us and be f-ed up as a result (ignoring the mysteriousness of incomplete penetrance).
Multiple mutations can cause GSDII, so its background rate is ~1 in 40,000. Since I only have the one mutation, pre-test the odds that a randomly selected partner and I would have had a child with GSDII were $\frac{1}{530}\cdot\frac{1}{4}=\frac{1}{2,120}$ and the odds of having a carrier child were $\frac{1}{530}\cdot\frac{1}{2}=\frac{1}{1,060}$. Post-test, these odds can be reduced to essentially zero if my partner were to do similar testing.
For my siblings, the odds of their children having GDSII with a randomly selected partner are $\frac{1}{530}\cdot\frac{1}{2}\cdot\frac{1}{4}=\frac{1}{4,240}$ and the odds of having a carrier child are $\frac{1}{530}\cdot\frac{1}{2}\cdot\frac{1}{2}=\frac{1}{2,120}$. The additional $\frac{1}{2}$ term being the odds they are also carriers, given Mendelian genetics. This is, of course, much higher than the $\frac{1}{40,000}$. So the test results in a big update for their state of knowledge.
I also tested negative for many things. For autosomal recessive disorders that means there's a ~0% chance of my children having them sans de novo mutation.
Updates from negative tests
But what can my siblings learn from my negative results? To figure this out, we need to pull out the Bayesian blender and pour (a) the background rate of the condition, (b) my parents' possible genotypes, and (c) Mendelian inheritance into it.
Let's call $p$ the frequency of carriers of a mutation in the population and $q=1-p$ the frequency of non-carriers.
Now, let's work through my parents' potential genotypes:
- Both parents non-carriers
- Prior probability: $q^2$
- Probability I'm a non-carrier given this scenario = 1
- Probability my siblings are non-carriers = 1
- One parent's a carrier, one's a non-carrier:
- Prior probability: $2pq$
- Probability I'm a non-carrier given this scenario = 1/2
- Probability my siblings are non-carriers = 1/2
- Both of my parents were carriers
- Prior probability: $p^2$
- Probability I'm a non-carrier given this scenario = 1/4
- Probability my siblings are non-carriers = 1/4
Now, Bayes' theorem says that
P(parental genotype | I'm a non-carrier) =
P(I'm a non-carrier | parental genotype)
* P(parental genotype) / P(I'm a non-carrier)
We have P(I'm a non-carrier) = $q^2\cdot1 + 2pq\cdot\frac{1}{2} \cdot p^2\cdot\frac{1}{4}=q^2+pq+p^2/4$.
Therefore, we have:
- P(both parents non-carriers | Me non-carrier) = $\frac{q^2}{q^2+pq+p^2/4}$
- P(one parent carrier | Me non-carrier) = $\frac{pq}{q^2+pq+p^2/4}$
- P(both carrier | Me non-carrier) = $\frac{p^2}{4}\frac{1}{q^2+pq+p^2/4}$
Now,
P(sib non-carrier) = Σ[P(sibling is non-carrier | parental genotype) * P(parental genotype | I'm a non-carrier)]
plugging it all in we get: $$\begin{aligned} P(\textrm{sib non-carrier}) &= \frac{q^2}{q^2+pq+p^2/4} \ &+ \frac{1}{2}\frac{pq}{q^2+pq+p^2/4} \ &+ \frac{1}{4}\frac{p^2}{4}\frac{1}{q^2+pq+p^2/4} \ &= \frac{q^2 + pq/2 + p^2/16}{q^2+pq+p^2/4} \end{aligned}$$
A mutation I don't have is Sandhoff disease which has a carrier frequency of between 1:310 to 1:276
Choosing the higher value, p=1/276, we plug and chug to get P(sib non-carrier)=99.8%. Before I did this test, q is reflective of the odds that my siblings would have been non-carriers: 99.6%. So the test represents a 0.2pp update for them.
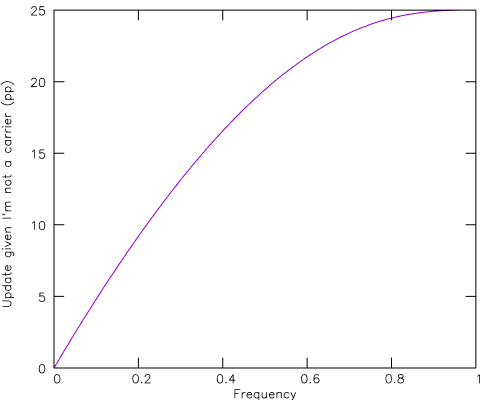
Gnuplot gives us the curve of the update equation:
set xrange [0:1];
set xlabel "Frequency"
set ylabel "Update given I'm not a carrier (pp)"
plot 100*(((1-x)**2 + x*(1-x)/2 + x**2/16)/((1-x)**2+x*(1-x)+x**2/4)-(1-x)) t ""
from which we see that we'd need a carrier frequency of 20-40% before we got significant updates.
We can also use this to double-check our work. At 0% frequency the update goes to 0 as it should. We can't really have a 100% frequency and meaningfully update, but consider 99.99% frequency. In this case either both my parents are carriers (very likely!) or only one of them is (very unlikely). My non-carrier status pins the unlikely scenario as the actual one so my siblings make a big 25pp update from believing they have a 25% chance of being a non-carrier to believing they have a 50% chance of being a non-carrier.